How to correctly use TF-IDF with imbalanced data
If you have been employing TF-IDF with imbalanced data while setting some hyper-parameter which limits the number of features used, then you are probably hurting your Machine Learning (ML) model’s performance by supplying an incorrect feature-set. In this article, I will show you a nifty trick that can get you back on track!
Note: Throughout this blog post, it is assumed that you are using the scikit-learn implementation of TF-IDF$^{[1]}$.
TF-IDF: An overview
TF-IDF stands for Term Frequency Inverse Document Frequency. To put it simply, TF-IDF returns a number (a scalar value) for every word that we have in a corpus (a set of documents) which denotes how important that given word is. It calculates this number/statistic using the following formula, $$\text{tfidf}(x,y) = \text{tf}(x,y) \times log \left( \frac{N}{\text{df}(x)} \right)$$where, $x$ is a word, $y$ is a document, $\text{tf}(x, y)$ is the frequency of word $x$ in document $y$, $N$ is the total number of documents and $\text{df}(x)$ is the number of documents containing the word $x$. Finally, $\text{tfidf}$ is the TF-IDF score for word $x$ in document $y$.
Here, the first term in the equation refers to term frequency while the second term refers to inverse document frequency. The two terms are exactly opposite in the way they assign importance to words.
Problem with Vanilla TF-IDF
It is very natural to limit the number of features representing a single document. This can be done by using either of the min_df, max_df or max_features hyper-parameters. For now, let us focus on max_features. The same logic will follow for the other two hyper-parameters as well.
The purpose of max_features is to limit the number of features (words) from the dataset for which we want to calculate the TF-IDF scores. This is done by choosing the features based on term frequency across the corpus$^{[1]}$.
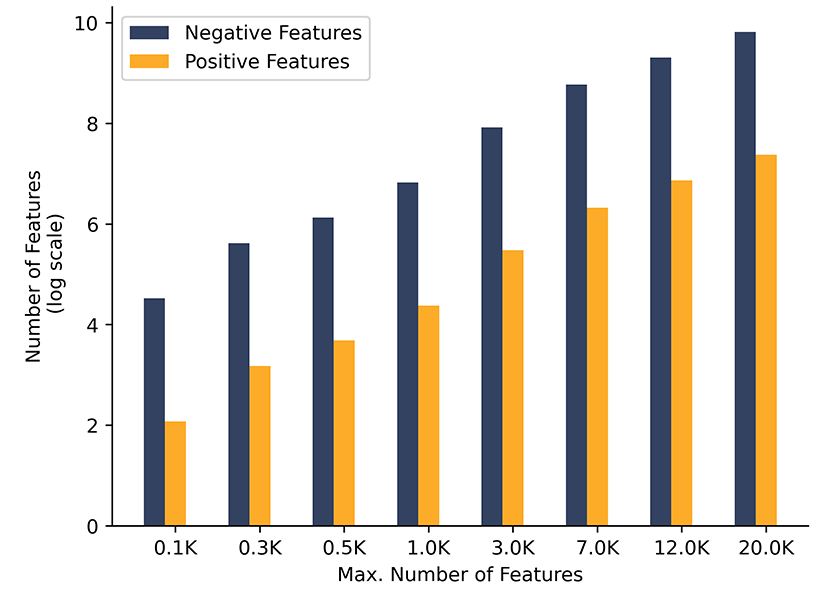
Why is this a problem? Consider you are working with the IMDB dataset and you need to predict whether a review is positive or negative. Assume that you sub-sampled the dataset in such a way that you ended up with $23$K negative reviews and $2$K positive reviews. Now if you run TF-IDF on top of this, with some value of max_features, there is a high chance that the majority of words chosen will be from the majority class (negative words/features). This makes sense since TF-IDF is selecting features based on term frequency alone and negative words are present in most of the samples. As a result, the minority class gets under-represented. This is demonstrated in Fig. 1, wherein it is clear that only after setting the max_features hyper-parameter to a really large value are the positive words selected as features by TF-IDF. This is not desirable as more features would require more samples, leading to curse of dimensionality.
Note: When creating Fig. 1, common words were excluded from the counting process.
Fig.1: As the max_features hyper-parameter is increased, no positive words/features are added into the feature-set until a very large value is reached
Intuition
We have now understood that TF-IDF does not correctly represent minority class words because it chooses features based on term frequency alone. So what can we do to ensure that we pick words from the minority class?
The first step is to understand that word frequencies between minority class and majority class are not comparable as majority class words will have a much higher frequency than the minority class. Thus, to represent both, we have to isolate the classes and then pick out the words. This way we ensure that we are selecting words from both majority and minority classes.
The next step will be to decide how many features we want to select. Let us say that we want a total of $300$ features (max_features=$300$). Out of this $300$ how do we decide on the number features that should be attributed to the majority and minority classes? We can take $150$ features per class but this will lead to under-representation of the majority class. Thus, some sort of weighting mechanism is required.
Solution: Weighted Class TF-IDF
Let us consider the following example. Assume there exists a dataset having two labels $0$ and $1$ with class $0$ containing $80\%$ of the samples while class $1$ containing the remaining $20\%$. Also, assume that max_features=$300$. At first, we calculate the weight for each label. Weight here refers to the number of features that should be selected from each class. Since class $0$ is present in $80\%$ of the records, we will pick $240$ features from class $0$ and $60$ features from class $1$. These values can be calculated based on the following formula, $$f_{c_i} = \text{max_features} \times \frac{n_{c_i}}{n_d}$$
Here, $n_{c_i}$ is the number of samples in the $i$-th class, $n_d$ is the total number of samples and $f_{c_i}$ is the number of features to be selected for the $i$-th class.
Now we run TF-IDF separately on class $0$ and class $1$ with max features set to $240$ and $60$, respectively. Further, in order to ensure non-overlapping feature-set between both classes, features selected in class $0$ are passed as stop-words to the stop_words hyperparameter when running TF-IDF over class $1$.
Once complete, we combine the vocabulary from both classes into a single list. This can be easily achieved since TF-IDF provides a vocabulary_ parameter that stores the entire vocabulary.
Finally, this combined vocabulary is used as the fixed vocabulary in another TF-IDF model which runs over the entire data. By fixing the vocabulary for the final TF-IDF run, we ensure that all documents/samples are represented by these words/features only.
This entire, novel process is called Weighted Class TF-IDF or WCTF-IDF. Thus, to put it simply the $300$ features chosen by WCTF-IDF are a better representation of the overall data as compared to the features chosen by the vanilla TF-IDF model. I shall prove this via empirical results.
Code
The code available here is to show the performance of WCTF-IDF on a single dataset. Results have been reported on other datasets as well.
Results
In this section, I have provided exhaustive empirical results to demonstrate the effectiveness of WCTF-IDF against TF-IDF in an imbalanced data setting. On average, WCTF-IDF outperforms TF-IDF by $4\%$ under the F1-score metric.
| Dataset | Class | Method | Precision | Recall | F1-Score | # samples |
|---|---|---|---|---|---|---|
| IMDB[2] | 0 | TF-IDF | 0.93 | 1.0 | 0.96 | 5750 |
| WCTF-IDF | 0.93 | 0.99 | 0.96 | |||
| 1 | TF-IDF | 0.74 | 0.15 | 0.25 | 500 | |
| WCTF-IDF | 0.75 | 0.19 | 0.31 |
Table 1: 25K negative reviews and 2K positive reviews were selected to generate an imbalanced version of the IMDB dataset. Best values are denoted in bold. WCTF-IDF clearly outperforms TF-IDF on all metrics for the minority class while achieving the same performance on the majority class.
| Dataset | Class | Method | Precision | Recall | F1-Score | # samples |
|---|---|---|---|---|---|---|
| Toxicity [3] Prediction |
0 | TF-IDF | 0.93 | 1.0 | 0.96 | 35837 |
| WCTF-IDF | 0.94 | 1.0 | 0.97 | |||
| 1 | TF-IDF | 0.93 | 0.36 | 0.52 | 4056 | |
| WCTF-IDF | 0.92 | 0.49 | 0.64 |
Table 2: Toxicity Prediction is a multilabel classification dataset. This was converted to a binary classification dataset by giving the label 1 to those samples having at least one of the following classes {toxic, severe_toxic, obscene, threat, insult, identity_hate}. Again it can be clearly understood that WCTF-IDF outperforms TF-IDF on all metrics for the minority class while achieving slightly better performance on the majority class as well. Best values are denoted in bold.
| Dataset | Class | Method | Precision | Recall | F1-Score | # samples |
|---|---|---|---|---|---|---|
| Sentiment140[4] | 0 | TF-IDF | 0.6 | 0.09 | 0.16 | 12500 |
| WCTF-IDF | 0.61 | 0.12 | 0.2 | |||
| 1 | TF-IDF | 0.91 | 0.99 | 0.95 | 112500 | |
| WCTF-IDF | 0.91 | 0.99 | 0.95 |
Table 3: WCTF-IDF once again outperforms TF-IDF on all metrics for the minority class while achieving same performance on the majority class. Best values are denoted in bold.
Ablation Study
Along with empirical results, I would also like to support my claim via in-depth analysis.
Running TF-IDF on the imbalanced version of the IMDB dataset and looking at the vocabulary list (note that only those words are being considered that appear in TF-IDF vocab but not in WCTF-IDF) shows that features are mostly composed of neutral or negative words such as {ridiculous, lack, cheap, ok, annoying, lost}. This makes sense because TF-IDF selects words simply on the basis of term frequency and a majority of the samples comprise of negative reviews. On the other hand, running WCTF-IDF results in mostly neutral or positive words (again, remember that only those words have been chosen that are present in WCTF-IDF vocab and not in TF-IDF) such as {loved, well, excellent, perfect, definitely, top, amazing, wonderful}. These positive words were not captured by the TF-IDF vocab as they were present in minority.
Fig. 2: As the max_features hyper-parameter is increased, WCTF-IDF selects the correct number of features in the minority class right from the start
Fig. 2 is in stark contrast to Fig. 1. Clearly, WCTF-IDF selects the representative number of features from the minority class while respecting the underlying class distribution. This is exactly what is required in an imbalanced data setting which further proves the efficacy of WCTF-IDF
Conclusion
Please find the link to the related GitHub repo here. The “demos” folder contains all of the remaining experiments in self-explanatory jupyter notebook files. Feel free to contribute to the repository if some enhancements and improvements can be made on the technique proposed above.